Difference between revisions of "Christoph Champ Logo"
(→The mathematics behind the logo) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 3: | Line 3: | ||
I have always been interested in geometry. This is especially true of symmetry. This is what I had in mind when I designed my logo for this site. It is actually just a Lissajous curve that has been transformed, using the principles of ''sumi-e'', for an artistic effect. | I have always been interested in geometry. This is especially true of symmetry. This is what I had in mind when I designed my logo for this site. It is actually just a Lissajous curve that has been transformed, using the principles of ''sumi-e'', for an artistic effect. | ||
| − | == The mathematics behind the logo == | + | ==The mathematics behind the logo== |
| − | In mathematics, a '''Lissajous curve''' is the graph of the system of parametric equations | + | In mathematics, a '''Lissajous curve''' is the graph of the system of parametric equations: |
<!--:<math>x=A\sin(at+\delta),\quad y=B\sin(bt),</math>--> | <!--:<math>x=A\sin(at+\delta),\quad y=B\sin(bt),</math>--> | ||
| Line 22: | Line 22: | ||
</pre> | </pre> | ||
| − | == Sandbox == | + | ==Sandbox== |
[[Image:Christoph Champ-beta.png]] | [[Image:Christoph Champ-beta.png]] | ||
| − | == External links == | + | ==External links== |
| − | * [ | + | *[[wikipedia:Lissajous curve]] |
| − | * [ | + | *[[wikipedia:Sumi-e]] |
| + | *[[wikipedia:Harmonograph]] | ||
[[Category:Personal]] | [[Category:Personal]] | ||
Latest revision as of 12:54, 24 December 2019
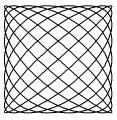
In case you are wondering what this site's logo (or Christoph Champ Logo / Sumi-e Lissajous curve) is all about, this article will attempt to explain it.
I have always been interested in geometry. This is especially true of symmetry. This is what I had in mind when I designed my logo for this site. It is actually just a Lissajous curve that has been transformed, using the principles of sumi-e, for an artistic effect.
The mathematics behind the logo
In mathematics, a Lissajous curve is the graph of the system of parametric equations:
- x = A*sin(at + δ), y = B*sin(bt),
Below is an example of a Lissajous figure with δ = π/2, a = 9, b = 8. Next to it is a sumi-e rendition of this same Lissajous curve (created by Christoph Champ).
You can easily generate a Lissajous curve in Maple by executing the following commands:
x1:= t->sin(9*t): y1:= t->sin(8*t):
plot({[x1(t), y1(t), t=0..2*Pi]});